After experiencing the new reentry effects introduced into the game (thank you Stef!) a couple of things struck me as a little.... off kilter.
In the tangible world the effects of the top 10% of a planets atmosphere is negligible, it's basically still a near vacuum, but in SFS the effects are almost immediate and spectacular.
Don't get me wrong, there's lots of things going on to cause these effects. A kilogram of matter re-entering the Earth's atmosphere at 1,600 m/s in SFS has 1.28 * 10⁶ joules of energy, so take your average capsule, parachute, heat shield package of 4.9 tons we get a whopping 6.272 * 10⁹ joules of energy. but like the ronco guy says, wait! there's more! This is just the kinetic energy, we've still got the little matter af the crafts mechanical energy to deal with as well. what's that you ask? well our craft is still sitting on top of a 30 km tall cliff. We calculate this little number and we add an additional 1.47 * 10⁸ kg/m or 1.442 * 10⁹ joules to the mix for a total of 7.713 * 10⁹ joules of energy to deal with.
Well hell yeah! that would explain the light show and with that much energy being thrown around we must be burning through velocity like mad! Right? Turns out that isn't quite the case. For the purposes of this discussion I quick saved a 4.9 ton craft entering Earth's atmosphere at an angle of 20° for repeatability as I gathered data.
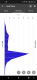
Turns out that the light show, despite being quite visually arresting doesn't have the same effect on our crafts velocity. I've got graphs galore but just showing the numbers at key points of our reentry shows some of the issues.
Firstly, at 27 km our temperature is ≈ 200° C and velocity has crept up to 2118 m/s in keeping with the real life model (kudos Stef!). Let's look at the data as we progress , 30 seconds in our temperature is 850° C progressing mostly linearly with some flattening to 2130° C at 90 seconds into reentry. At our peak energy consumption we're only consuming 7.89 * 10⁷ joules a second, certainly enough to power a light show but barely putting a damper on our velocity.
Alright, now we know what we're dealing with what can we do with it? Since we neglected to carry the equivalent fuel required to get us here and meany Stef won't let us deploy our parachute in a vacuum or at supersonic speeds, we're going to need something to slow us down.
There are 2 basic atmospheric reentry approaches, ballistic and lifting. A lifting approach entails entering an atmosphere at a shallow enough angle of incidence the craft exits the atmosphere rather than continuing in the direction of the retarding force.
We're going to examine the ballistic approach.
Ever since cannoneers began to analyze the trajectories of cannonballs we've quantified the forces acting on an object traveling through the atmosphere.
!!! CAUTION MATH AHEAD !!!
The 3 basic formulas I applied are:
equation of motion
a = ½ P * v² * Cᵈ * A
m
where a is the angle of flight, P is atmospheric density, v is velocity, Cᵈ is coefficient of drag, I used the Cᵈ of the Mercury capsule 1.6, A is area and m is mass
ballistic coefficient. A measure of a body's ability to overcome air resistance in flight.
B ᶜ = m
Cᵈ * A
where m = mass, Cᵈ is coefficient of drag and A is area
and finally, Fᵈ the drag force on our vehicle.
Fᵈ = ½ P * V² * Cᵈ * A
So if we look at the data now the numbers begin to align. The key factor being P, atmospheric pressure.
Running the numbers again, we see, at the beginning of our entry, due to minimal atmospheric pressure the effects of drag are negligible;
Fᵈ = ½ .000001 * 2,114 m/s² * 1.6 * 3.14 = 22.45 joules. Once we get into the thick of things, so to speak, we find that joules, and velocity, bleed off rapidly
Fᵈ = ½ .8 * 1,644 m/s * 1.6 * 3.14 = 5.431 * 10⁶ joules and our velocity ( and the force required to slow us) is dropping rapidly.
In conclusion, if you've made it this far, all is well with the laws of physics in the SFS world in regards to atmospheric reentry. (apologies Stef but I had to check)
I believe my misperception was caused by a time dilation effect the visuals created. I simply perceived time to be moving much faster than it actually was.
My apologies for any errors in notation, an unfortunate limitation of my keyboard. Any errors in math are my own as well.
references include but are not limited to:
Wikipedia, the free encyclopedia › wiki
Atmospheric entry - Wikipedia
Conquering the fast and the furious: Physics of atmospheric re-entry – theGIST
https://www.faa.gov › mediaPDF
Returning from Space: Re-entry - FAA
In the tangible world the effects of the top 10% of a planets atmosphere is negligible, it's basically still a near vacuum, but in SFS the effects are almost immediate and spectacular.
Don't get me wrong, there's lots of things going on to cause these effects. A kilogram of matter re-entering the Earth's atmosphere at 1,600 m/s in SFS has 1.28 * 10⁶ joules of energy, so take your average capsule, parachute, heat shield package of 4.9 tons we get a whopping 6.272 * 10⁹ joules of energy. but like the ronco guy says, wait! there's more! This is just the kinetic energy, we've still got the little matter af the crafts mechanical energy to deal with as well. what's that you ask? well our craft is still sitting on top of a 30 km tall cliff. We calculate this little number and we add an additional 1.47 * 10⁸ kg/m or 1.442 * 10⁹ joules to the mix for a total of 7.713 * 10⁹ joules of energy to deal with.
Well hell yeah! that would explain the light show and with that much energy being thrown around we must be burning through velocity like mad! Right? Turns out that isn't quite the case. For the purposes of this discussion I quick saved a 4.9 ton craft entering Earth's atmosphere at an angle of 20° for repeatability as I gathered data.
Turns out that the light show, despite being quite visually arresting doesn't have the same effect on our crafts velocity. I've got graphs galore but just showing the numbers at key points of our reentry shows some of the issues.
Firstly, at 27 km our temperature is ≈ 200° C and velocity has crept up to 2118 m/s in keeping with the real life model (kudos Stef!). Let's look at the data as we progress , 30 seconds in our temperature is 850° C progressing mostly linearly with some flattening to 2130° C at 90 seconds into reentry. At our peak energy consumption we're only consuming 7.89 * 10⁷ joules a second, certainly enough to power a light show but barely putting a damper on our velocity.
Alright, now we know what we're dealing with what can we do with it? Since we neglected to carry the equivalent fuel required to get us here and meany Stef won't let us deploy our parachute in a vacuum or at supersonic speeds, we're going to need something to slow us down.
There are 2 basic atmospheric reentry approaches, ballistic and lifting. A lifting approach entails entering an atmosphere at a shallow enough angle of incidence the craft exits the atmosphere rather than continuing in the direction of the retarding force.
We're going to examine the ballistic approach.
Ever since cannoneers began to analyze the trajectories of cannonballs we've quantified the forces acting on an object traveling through the atmosphere.
!!! CAUTION MATH AHEAD !!!
The 3 basic formulas I applied are:
equation of motion
a = ½ P * v² * Cᵈ * A
m
where a is the angle of flight, P is atmospheric density, v is velocity, Cᵈ is coefficient of drag, I used the Cᵈ of the Mercury capsule 1.6, A is area and m is mass
ballistic coefficient. A measure of a body's ability to overcome air resistance in flight.
B ᶜ = m
Cᵈ * A
where m = mass, Cᵈ is coefficient of drag and A is area
and finally, Fᵈ the drag force on our vehicle.
Fᵈ = ½ P * V² * Cᵈ * A
So if we look at the data now the numbers begin to align. The key factor being P, atmospheric pressure.
Running the numbers again, we see, at the beginning of our entry, due to minimal atmospheric pressure the effects of drag are negligible;
Fᵈ = ½ .000001 * 2,114 m/s² * 1.6 * 3.14 = 22.45 joules. Once we get into the thick of things, so to speak, we find that joules, and velocity, bleed off rapidly
Fᵈ = ½ .8 * 1,644 m/s * 1.6 * 3.14 = 5.431 * 10⁶ joules and our velocity ( and the force required to slow us) is dropping rapidly.
In conclusion, if you've made it this far, all is well with the laws of physics in the SFS world in regards to atmospheric reentry. (apologies Stef but I had to check)
I believe my misperception was caused by a time dilation effect the visuals created. I simply perceived time to be moving much faster than it actually was.
My apologies for any errors in notation, an unfortunate limitation of my keyboard. Any errors in math are my own as well.
references include but are not limited to:
Wikipedia, the free encyclopedia › wiki
Atmospheric entry - Wikipedia
Conquering the fast and the furious: Physics of atmospheric re-entry – theGIST
https://www.faa.gov › mediaPDF
Returning from Space: Re-entry - FAA